📝 This post was initially released on the HLS Works Blog in 2020. The post was moved to this website after HLS Works closed in Sep 2021.

Why use HLS data types⌗

The C/C++ language has many data types that most people are familiar with, from the basic ones, char, int, unsigned, and float, to the bit accurate std types, including int8_t, int32_t, and more. If there are so many data types to choose from, why would we even bother with new ones? What are the advantages of HLS types? How can these data types be used effectively? These questions will be answered in this post.

Types⌗

Arbitrary Bit Width Integer⌗

The Xilinx arbitrary library provides two arbitrary types: ap_int for signed integers, and ap_uint for unsigned integers. The major advantage of HLS types over standard data types is that it generates more efficient and accurate hardware, as Xilinx states. Another advantage of HLS types over other data types is the ability to create integers of any width. But, keep in mind that the wider (more bits) the data type is, the more complex it is to operate, store, and route.

#include "ap_int.h"

constexpr int G_MAX_IMAGE_WIDTH  = 100;
constexpr int G_MAX_IMAGE_HEIGHT = 10;

//BITS is the number of bits to store n
template<typename T>
constexpr T BITS(T n){ return (n<=1? 1 : BITS(n/2)+1); }

int main(){
    using ui32 = ap_uint<32>; //Better than unsigned int or int32_t
    ap_int<1>   boolean = false;
    ap_int<32>  simple = 55;
    ap_uint<128> wide("123456789123456789123456789", 10); // big number (it does not fit in a int64)
    ap_uint<3>  weight = 0b001; // small bit-wide types are commonly used, among others, in AI quantized models.
    ap_int<8>   byte = 0xFF;

    typedef struct {
        ap_int<BITS(G_IMAGE_WIDTH)>  width;
        ap_int<BITS(G_IMAGE_HEIGHT)> height;
    } ImgSize;
    return 0;
}

Another great feature offered by the Xilinx library is the way in which ap_int and ap_uint treats return types for operations. When operating standard types, the return type is the same as the operands, leading to overflows (either positive or negative). For example, the addition of two chars of value 200 also returns a char, but such a type cannot store the result since the upper limit for a char is 255. On the other hand, HLS data types avoid losing information. The result of an operation will be of a type capable of storing any possible result, no matter the values of the operands. For instance, the addition of two ap_int<8> is an ap_int<9> that cannot overflow, no matter the values of the operads. In the same manner, the multiplication results in an ap_int<16>. Mixing signed and unsigned types will return a signed type, e.g., ap_int<8> plus ap_uint<8> is an ap_int<10>, and so on.

#include <iostream>
#include "ap_int.h"
#include "hws_utils.h"

int main(){
    ap_int<8> i8;
    ap_uint<8> u8;

    cout << TypeInfo< decltype(u8 + u8) >::name() << endl;
        // ap_uint<9>
    cout << TypeInfo< decltype(u8 * u8) >::name() << endl;
        // ap_uint<16>
    cout << TypeInfo< decltype(u8 + i8) >::name() << endl; // u8 to integer is i9, i9+i8 = i10
        // ap_uint<10>

    return 0;
}

template<typename T>
struct TypeInfo;

template<int W>
struct TypeInfo<ap_int<W>>{
    static std::string Name(){
        std::stringstream  os;
        os << "ap_int<" << W << ">";
        return os.str();
    }
};
template<int W>
struct TypeInfo<ap_uint<W>>{
    static std::string Name(){
        std::stringstream  os;
        os << "ap_uint<" << W << ">";
        return os.str();
    }
};

Fixed Bit Width Type⌗

Fixed point arithmetics are essential in hardware development. This is a much simpler alternative to floating-point arithmetics while being more versatile than integers, though C/C++ does not contain types supporting fixed-point arithmetics. Implementing floating-point arithmetics requires complex logic, even with DSP (in Xilinx devices, the DSP48). However, the new Xilinx Versal lineup includes a more versatile DSP, the DSP58e, that is capable of operating floating-point data.

The Xilinx arbitrary point library allows developers to use fixed-point data, but the utility of this library does not stop here. The library also includes many other features to craft the behavior of fixed-point data types. When declaring an ap_fixed or ap_ufixed (the latter for unsigned fixed-point values), it is possible to choose among different overflow and rounding (quantization, as Xilinx refers to it) modes.

The ap_fixed comes in the shape of a template type, in which the first two template arguments are the total bit width (W), and the integer width (I). The former is the number of bits occupied by the type, and the latter is the number of bits used to represent the integer part (See figure 1). The following two arguments are also mandatory and serve to specify the overflow (O) and rounding (Q) modes (see Table 1). Xilinx states that AP_SAT requires extra hardware that can increase LUT utilization up to 20%. When resource utilization is not a concern, my personal preferences are AP_SAT (saturation) and SC_RND_CONV (convergent rounding). Otherwise, the default (AP_WRAP and SC_TRUNC) modes will work just fine. The last argument is optional and only makes sense when used alongside the AP_WRAP mode. I do not find this argument particularly useful, so I leave it set to the default value (0) or a value equal to the integer width (I). If you are unfamiliar with these overflow and rounding methods, there are examples of each method in UG1399 pages 516 to 519.

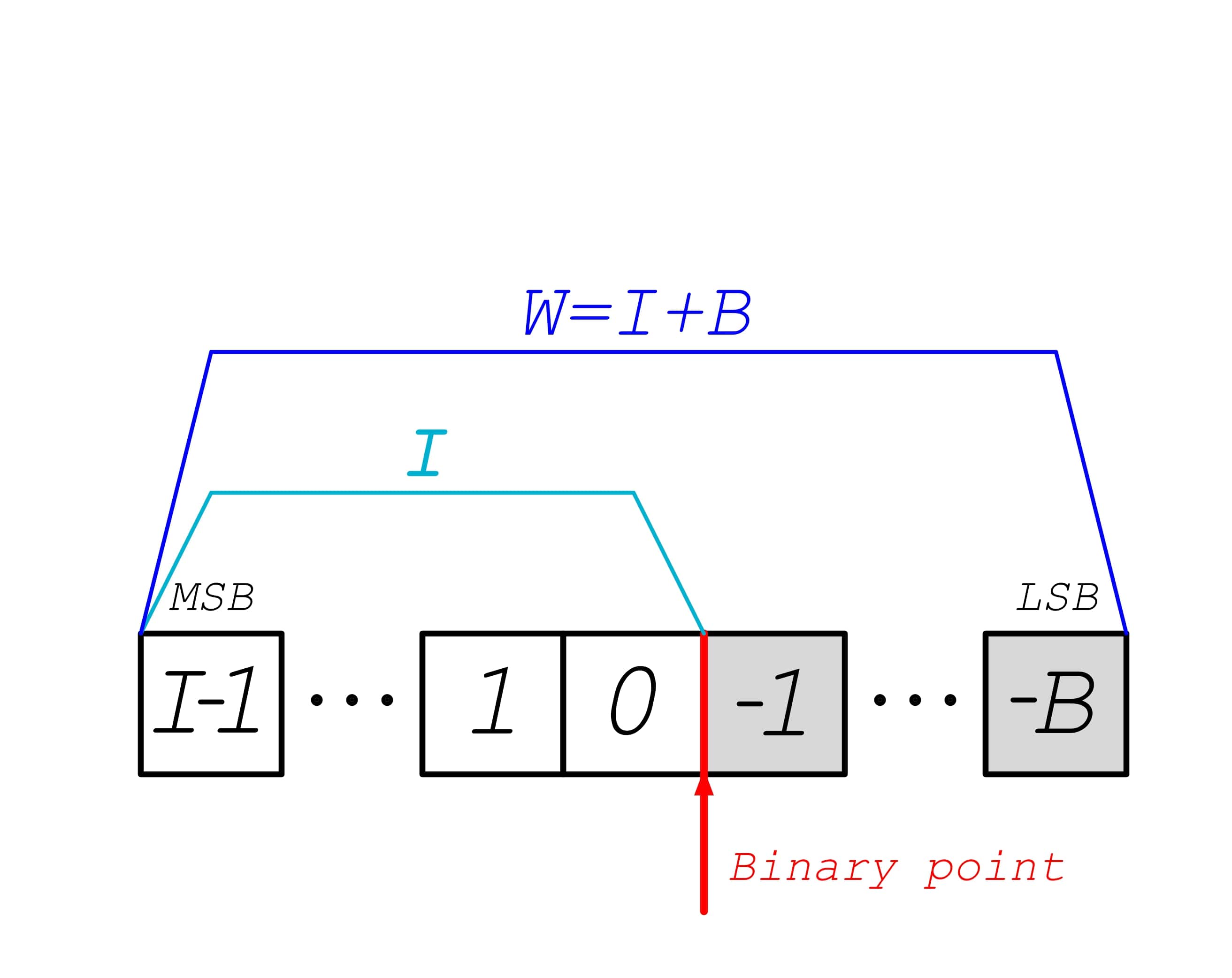
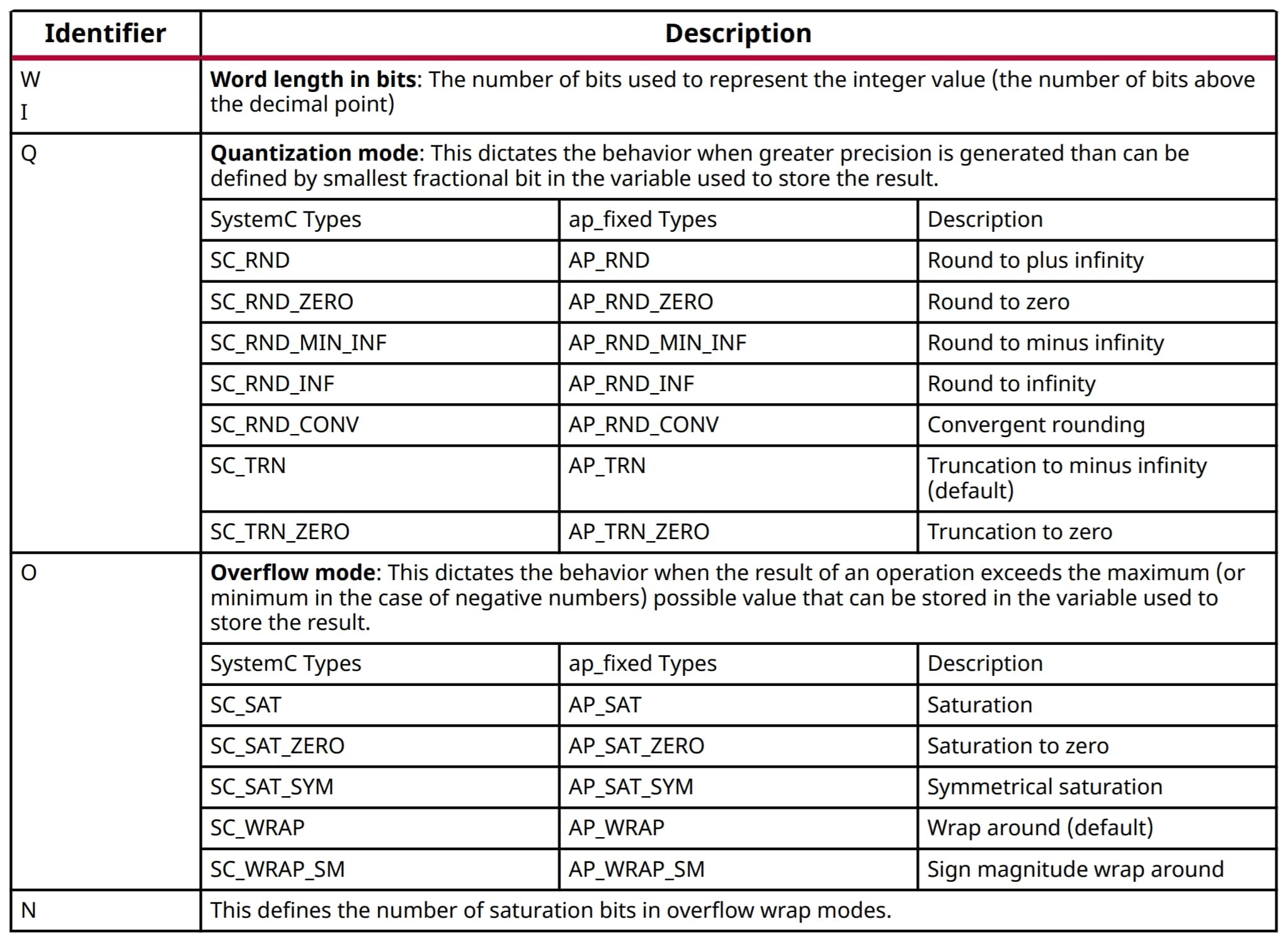
In Table 1, the second column (ap_fixed Types) lists the option aliases for C/C++, while the first column (System C Types) is for System C. Let’s see some examples.

ap_fixed<10, 10, AP_RND_CONV, AP_SAT> integer;
ap_ufixed<10, 5, AP_RND, AP_WRAP> ufixed;

ap_ufixed<10, 5, AP_RND, AP_SAT>    fx10;
ap_ufixed<5, 5, AP_RND, AP_WRAP, 5> fx5;
ap_ufixed<8, 4, AP_RND, AP_WRAP, 3> fx8;

Another great feature is that the resulting ap_fixed of mixing types in a mathematical expression can losslessly contain any possible result, as it happens with ap_int. This occurs in the same way as with ap_int. First, mixing signed and unsigned types will result in a signed type. Second, the resulting type total and integer width parameters will be large enough to store any result.

However, there is a warning regarding the rounding and overflow parameters, which are set to the default values independently of the operands. This occurs even when mixed types only differ in bit widths (see the second example below).

cout << TypeInfo< decltype(fx10) >::Name() << endl;
    // ap_ufixed<10, 5, SC_RND, SC_SAT>
cout << TypeInfo< decltype(fx10 + fx10) >::Name() << endl; 
    // ap_ufixed<11, 5, SC_TRN, SC_WRAP>
cout << TypeInfo< decltype(fx10 + u8) >::Name() << endl;
    // ap_ufixed<9, 9, SC_TRN, SC_WRAP>

Finally, it is worth mentioning that mixing fixed and integer types is possible! That is because an integer can be represented by an ap_fixed with equal total and integer widths.

Tricks⌗

Accessing a Specific Bit⌗

Accessing a specific bit is quite simple using the operator [], which returns a reference to the specified bit. Accessing a specific bit is quite simple using the operator [], which returns a reference to the specified bit. Since the operator returns a reference, we can either read or write to the specified bit.

ap_int<8> pp = 0;

// On the left side
pp[4] = 1; //MSB
pp[0] = 1; //LSB

// On the right side
if(pp[0]) cout << "hello" << endl;

Accessing Ranges of Bits⌗

Ranges of bits can be accessed using the method range(Hi, Low), or in a more straightforward manner, the operator (Hi, Low), which takes the subvector [Hi:Low] with boundaries included. For example, num.range(9, 5) or num(9, 5) is a vector with references to bits 3, 2, and 1 from MSB to LSB.

ap_ufixed<5, 5, AP_RND, AP_WRAP> integerPart    = 2;
ap_ufixed<5, 0, AP_RND, AP_WRAP> fractionalPart = .25;
ap_ufixed<10, 5, AP_RND, AP_WRAP> num;

// On the left side
num.range(9, 5) = integerPart; // Using "range" method
num(4, 0) = fractionalPart;    // Using operator ()

// On the right side
if(num.range(9, 5) == 2) cout << "Value = " << num << endl;

Using ap_fixed to Enhance Integers⌗

A helpful trick is using an ap_fixed with equal data and integer widths instead of an ap_int to create an integer. The ap_fixed enables controlling the rounding and quantization modes; We don’t have such control with ap_int.

ap_int<W> iW;
ap_fixed<W, W, AP_RND_CONV, AP_SAT> iW2; // Now we can change modes

Converting to C/C++ Types⌗

HLS types support implicit conversions for most types, but you can also explicitly convert these data types using the methods to_<type>(); for example, to_char, to_int, to_uint, to_int64, to_uint64, to float, and to_half. When converting data types, note that truncation is used instead of the selected rounding mode.

ap_int<9> c1("0b100000001");
ap_ufixed<15, 10, AP_RND, AP_WRAP> c2 = 7.75;

char cc1 = c1.to_char()+'0';
cout << "cc1 = " << cc1 << endl;
    // cc1 = 1
int cc2 = c2.to_int();
cout << "cc2 = " << cc2 << endl;
    // cc2 = 7

Console Printing⌗

Hardware development involves dealing with bit vectors, and representing this data in binary or hexadecimal formats is clearer than using the decimal format. Fortunately, the presented HLS types (ap_int and ap_fixed) can be printed as standard types. In addition, the iomanip library helps with formating the printed output, e.g. limiting the number of digits or choosing the adecuate base, among other features. Some of these capabilities are demonstrated in the example below.

#include <iomanip>

ap_int<16> aa = 255;

cout << aa << endl; // base 10 by default
    // 255
cout << setbase(16) << aa << endl; // Supports Hex, Oct, Dec but not Binary
    // 0xFF
cout << aa.to_string() << endl; // though, you can use to_string( base ); base is 2 by default
    // 0b11111111
printf("%s\n", aa.to_string(10).c_str()); // Or base 10
    // 255